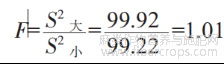摘 要:为建立一种快速有效测定苎麻单纤维断裂强力回归模型法,采用传统国标法测定苎麻单纤维断裂强力,用纤维细度仪测出纤维细度,SPSS19.0统计软件分析二者的相关性,拟合出5个回归模型。确定苎麻单纤维断裂强力与纤维细度最佳回归模型为:Y=107.58-0.054X+8.55×10-6X2。F检验和t检验证明该方法与传统国标法差异不显著。因此,通过纤维细度仪测试纤维细度,再经回归模型的换算,可同步实现苎麻单纤维断裂强力的自动化快速检测。
关键词:苎麻单纤维;断裂强力;回归模型;构建
苎麻纤维强力是评价衡量苎麻纤维拉伸断裂性能最主要的品质指标,纤维强力越好,其韧性和可纺性能越好。目前,测定苎麻单纤维强力主要依据国家标准《苎麻单纤维断裂强力试验方法GB5886—1986》(以下简称国标法),由于苎麻纤维本身的不均匀性,该法规定测定一个苎麻单纤维样品,需要通过人工在纤维强力仪上拉伸断裂测定500根以上纤维强力,计算500根以上纤维断裂强力的平均值,再通过测定的相应细度计算出其纤维强度。该方法劳动强度大、耗时费力;鉴于上述,通过苎麻纤维细度与其单纤维断裂强力相关性分析,构建一种基于苎麻单纤维强力快速模型法,即通过纤维细度仪快速测定出苎麻纤维细度代入其回归模型,得出苎麻单纤维断裂强力,以解决传统国标法(GB5886—1986)测量苎麻单纤维强力耗时长的问题,为苎麻单纤维强力测定提供一种快速回归模型法,特别适合大批量样品纤维断裂强力的分析[1-2]。
1试验设计
传统国标法测定苎麻单纤维纤维断裂强度,纤维细度仪测定纤维细度。将获得的纤维断裂强力与纤维细度数据用SPSS19.0统计软件拟合分析,建立5个回归模型。根据回归模型单调性与相关系数优化回归方程。根据优化的回归方程,纤维线密度可以通过纤维直径的测试结果计算得到。为比较模型法与传统国标法的差异,同时设计对比试验,采用F检验和t检验来分析评价2种方法的差异显著性。
2试验方法
2.1材料与设备
284个苎麻纤维(其中:264个用于构建回归模型;20个用于与传统方法对比研究,评价差异显著性),均为农业部麻类产品质量监督检验测试中心存留样品。
BFU-1型麻纤维细度自动分析仪(农业部麻类产品质量监督检验测试),北京合众视野有限公司产品,有效测量细度范围为200~8000m/g;1.0mm纤维切割器;1mm纤维散播器;YM-06D型单纤维电子强力仪,山东元茂纺织仪器有限公司产品;专用纤维希梳(10针/cm)。全程试验在恒温恒湿的纤维实验室进行(温度20±2℃,湿度65%±3%)。
2.2方法与过程
2.2.1回归模型的建立和优化
(1)苎麻单纤维强力测定。参照国标法,从苎麻纤维样品中部剪取10cm长,用专用纤维希梳梳理,使纤维完全分散。从梳理好的纤维中随机抽取测定500根纤维强力,取纤维强力平均值作为样品测定结果[3]。
(2)苎麻纤维细度测定。参照《苎麻纤维细度快速测定方法》(NY/T1538—2007),用纤维切割器将步骤1的对应试样剪切成1mm长的纤维碎段,用撒播器均匀分散在载玻片上,每个片上有5000~8000根纤维碎段。将载玻片放在纤维细度仪上扫描测试纤维细度[4]。
2.2.2模型法与传统国标法差异显著性比较
取20个苎麻纤维样品分别采用传统国标法测试与模型法计算单纤维强力。用F检验和t检验评价这2种方法的差异显著性。
3结果与分析
3.1回归模型优化和相关性分析[5]
纤维断裂强力(Y)与细度(X)测定结果见表1。
表1纤维断裂强力(Y)与细度(X)测定结果
|
1 |
46.63 |
1407 |
67 |
38.53 |
17 |
93 |
133 |
47.50 |
1372 |
199 |
27.91 |
2176 |
||||
|
样品编号 |
Y(cN) |
X/m |
g-1 |
样品编号 |
Y(cN) |
X/m |
g-1 |
样品编号 |
Y(cN) |
X/m |
g-1 |
样品编号 |
Y(cN) |
X/m |
g-1 |
|
|
2 |
46.63 |
1416 |
68 |
38.51 |
17 |
95 |
134 |
47.32 |
1376 |
200 |
27.90 |
2178 |
||||
|
3 |
46.56 |
1419 |
69 |
38.37 |
18 |
08 |
135 |
47.26 |
1385 |
201 |
27.69 |
2184 |
||||
|
4 |
46.52 |
1421 |
70 |
38.18 |
18 |
08 |
136 |
46.95 |
1388 |
202 |
27.63 |
2192 |
||||
|
5 |
46.51 |
1422 |
71 |
38.17 |
18 |
19 |
137 |
46.75 |
1392 |
203 |
27.57 |
2200 |
||||
|
6 |
46.41 |
1428 |
72 |
38.06 |
18 |
23 |
138 |
46.71 |
1394 |
204 |
27.57 |
2207 |
||||
|
7 |
46.32 |
1431 |
73 |
37.88 |
18 |
29 |
139 |
26.17 |
2487 |
205 |
27.56 |
2207 |
||||
|
8 |
46.26 |
1433 |
74 |
37.87 |
18 |
30 |
140 |
26.14 |
2499 |
206 |
27.53 |
2209 |
||||
|
9 |
46.05 |
1438 |
75 |
37.87 |
18 |
42 |
141 |
26.14 |
2522 |
207 |
26.38 |
2438 |
||||
|
10 |
45.46 |
1531 |
76 |
37.84 |
18 |
46 |
142 |
25.40 |
2525 |
208 |
26.32 |
2460 |
||||
|
11 |
45.34 |
1532 |
77 |
37.48 |
18 |
46 |
143 |
25.40 |
2578 |
209 |
26.18 |
2470 |
||||
|
12 |
45.29 |
1533 |
78 |
37.42 |
18 |
51 |
144 |
25.39 |
2659 |
210 |
26.18 |
2472 |
||||
|
13 |
45.23 |
1534 |
79 |
37.30 |
18 |
57 |
145 |
25.06 |
2727 |
211 |
31.37 |
2057 |
||||
|
14 |
45.21 |
1542 |
80 |
37.28 |
18 |
61 |
146 |
25.06 |
2941 |
212 |
31.37 |
2067 |
||||
|
15 |
45.00 |
1542 |
81 |
37.12 |
18 |
72 |
147 |
25.05 |
3197 |
213 |
31.30 |
2068 |
||||
|
16 |
44.99 |
1545 |
82 |
36.98 |
18 |
73 |
148 |
36.79 |
1876 |
214 |
31.13 |
2068 |
||||
|
17 |
44.94 |
1546 |
83 |
34.04 |
19 |
84 |
149 |
36.62 |
1877 |
215 |
31.12 |
2069 |
||||
|
18 |
44.94 |
1555 |
84 |
33.67 |
19 |
86 |
150 |
36.48 |
1879 |
216 |
31.06 |
2081 |
||||
|
19 |
44.90 |
1556 |
85 |
33.67 |
19 |
91 |
151 |
36.29 |
1883 |
217 |
30.95 |
2083 |
||||
|
20 |
44.81 |
1564 |
86 |
33.63 |
19 |
91 |
152 |
36.10 |
1886 |
218 |
30.71 |
2088 |
||||
|
21 |
44.76 |
1565 |
87 |
33.48 |
19 |
92 |
153 |
36.04 |
1888 |
219 |
30.45 |
2094 |
||||
|
22 |
44.58 |
1566 |
88 |
33.25 |
19 |
94 |
154 |
36.03 |
1900 |
220 |
30.12 |
2096 |
||||
|
23 |
44.28 |
1566 |
89 |
33.23 |
19 |
94 |
155 |
36.01 |
1900 |
221 |
29.84 |
2097 |
||||
|
24 |
41.38 |
1678 |
90 |
33.22 |
19 |
94 |
156 |
35.82 |
1912 |
222 |
29.79 |
2098 |
||||
|
25 |
41.21 |
1678 |
91 |
33.22 |
19 |
99 |
157 |
35.80 |
1914 |
223 |
44.16 |
1567 |
||||
|
26 |
41.03 |
1680 |
92 |
40.52 |
17 |
29 |
158 |
35.72 |
1916 |
224 |
44.12 |
1572 |
||||
|
27 |
41.00 |
1680 |
93 |
40.51 |
17 |
29 |
159 |
35.54 |
1927 |
225 |
43.99 |
1572 |
||||
|
28 |
41.00 |
1685 |
94 |
40.41 |
17 |
32 |
160 |
33.03 |
2006 |
226 |
43.98 |
1572 |
||||
|
29 |
40.96 |
1692 |
95 |
40.41 |
17 |
33 |
161 |
32.96 |
2007 |
227 |
43.82 |
1583 |
||||
|
30 |
40.95 |
1694 |
96 |
40.27 |
17 |
35 |
162 |
32.85 |
2008 |
228 |
43.71 |
1588 |
||||
|
31 |
40.89 |
1695 |
97 |
40.11 |
17 |
36 |
163 |
32.78 |
2013 |
229 |
43.69 |
1593 |
||||
|
32 |
40.88 |
1697 |
98 |
40.11 |
17 |
36 |
164 |
32.78 |
2013 |
230 |
43.64 |
1595 |
||||
|
33 |
40.87 |
1700 |
99 |
40.09 |
17 |
45 |
165 |
32.63 |
2015 |
231 |
43.59 |
1595 |
||||
|
34 |
40.75 |
1702 |
100 |
40.00 |
17 |
55 |
166 |
32.58 |
2018 |
232 |
46.01 |
1445 |
||||
|
35 |
40.73 |
1710 |
101 |
39.95 |
17 |
58 |
167 |
32.52 |
2019 |
233 |
45.96 |
1454 |
||||
|
36 |
40.67 |
1713 |
102 |
39.29 |
17 |
58 |
168 |
32.52 |
2022 |
234 |
45.94 |
1459 |
||||
|
37 |
40.63 |
1721 |
103 |
39.19 |
17 |
66 |
169 |
32.34 |
2038 |
235 |
45.94 |
1464 |
||||
|
38 |
57.85 |
1160 |
104 |
38.91 |
17 |
67 |
170 |
31.79 |
2038 |
236 |
45.90 |
1466 |
||||
|
样品编号 |
Y(cN) |
X/m |
g-1 |
样品编号 |
Y(cN) |
X/m |
g-1 |
样品编号 |
Y(cN) |
X/m |
g-1 |
样品编号 |
Y(cN) |
X/m |
g-1 |
|
|
39 |
55.81 |
1188 |
105 |
38.89 |
17 |
73 |
171 |
31.63 |
2044 |
237 |
45.90 |
1467 |
||||
|
40 |
54.77 |
1204 |
106 |
27.49 |
22 |
23 |
172 |
31.55 |
2052 |
238 |
45.84 |
1470 |
||||
|
41 |
52.98 |
1251 |
107 |
27.31 |
22 |
39 |
173 |
26.54 |
2351 |
239 |
45.76 |
1486 |
||||
|
42 |
52.37 |
1256 |
108 |
27.11 |
22 |
42 |
174 |
26.54 |
2388 |
240 |
45.73 |
1488 |
||||
|
43 |
50.96 |
1260 |
109 |
27.11 |
22 |
42 |
175 |
26.53 |
2391 |
241 |
45.65 |
1495 |
||||
|
44 |
49.96 |
1279 |
110 |
27.10 |
22 |
56 |
176 |
26.50 |
2405 |
242 |
45.54 |
1496 |
||||
|
45 |
49.77 |
1280 |
111 |
26.75 |
22 |
76 |
177 |
26.39 |
2406 |
243 |
45.52 |
1510 |
||||
|
46 |
49.20 |
1298 |
112 |
26.75 |
22 |
90 |
178 |
26.39 |
2416 |
244 |
45.51 |
1520 |
||||
|
47 |
49.10 |
1335 |
113 |
26.74 |
23 |
04 |
179 |
35.46 |
1927 |
245 |
29.79 |
2104 |
||||
|
48 |
48.99 |
1336 |
114 |
26.74 |
23 |
24 |
180 |
35.43 |
1927 |
246 |
29.53 |
2107 |
||||
|
49 |
48.93 |
1342 |
115 |
26.74 |
23 |
26 |
181 |
35.34 |
1930 |
247 |
29.39 |
2111 |
||||
|
50 |
48.72 |
1344 |
116 |
26.73 |
23 |
38 |
182 |
35.29 |
1940 |
248 |
29.38 |
2114 |
||||
|
51 |
42.97 |
1619 |
117 |
41.89 |
16 |
66 |
183 |
35.09 |
1944 |
249 |
29.16 |
2116 |
||||
|
52 |
42.97 |
1624 |
118 |
41.87 |
16 |
68 |
184 |
34.98 |
1949 |
250 |
28.76 |
2126 |
||||
|
53 |
42.92 |
1634 |
119 |
41.77 |
16 |
69 |
185 |
34.72 |
1950 |
251 |
28.55 |
2129 |
||||
|
54 |
42.80 |
1634 |
120 |
41.74 |
16 |
72 |
186 |
34.50 |
1953 |
252 |
28.55 |
2134 |
||||
|
55 |
42.70 |
1637 |
121 |
41.53 |
16 |
72 |
187 |
34.38 |
1956 |
253 |
28.54 |
2136 |
||||
|
56 |
42.67 |
1638 |
122 |
41.50 |
16 |
76 |
188 |
34.31 |
1962 |
254 |
28.28 |
2140 |
||||
|
57 |
42.64 |
1642 |
123 |
41.44 |
16 |
78 |
189 |
34.30 |
1964 |
255 |
28.16 |
2142 |
||||
|
58 |
42.47 |
1642 |
124 |
48.33 |
13 |
45 |
190 |
34.25 |
1973 |
256 |
43.58 |
1595 |
||||
|
59 |
42.38 |
1646 |
125 |
48.33 |
13 |
47 |
191 |
34.11 |
1975 |
257 |
43.42 |
1596 |
||||
|
60 |
42.32 |
1647 |
126 |
48.30 |
13 |
48 |
192 |
34.06 |
1978 |
258 |
43.40 |
1598 |
||||
|
61 |
42.30 |
1649 |
127 |
48.25 |
13 |
56 |
193 |
34.04 |
1982 |
259 |
43.31 |
1599 |
||||
|
62 |
42.22 |
1652 |
128 |
48.20 |
13 |
65 |
194 |
28.16 |
2146 |
260 |
43.30 |
1599 |
||||
|
63 |
42.20 |
1655 |
129 |
48.07 |
13 |
67 |
195 |
28.15 |
2161 |
261 |
43.26 |
1605 |
||||
|
64 |
41.93 |
1660 |
130 |
48.01 |
13 |
67 |
196 |
27.95 |
2161 |
262 |
43.13 |
1611 |
||||
|
65 |
38.86 |
1785 |
131 |
47.96 |
13 |
71 |
197 |
27.95 |
2168 |
263 |
43.06 |
1613 |
||||
|
66 |
38.59 |
1793 |
132 |
47.61 |
13 |
72 |
198 |
27.94 |
2175 |
264 |
43.01 |
1614 |
||||
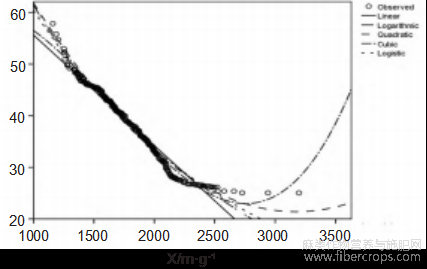
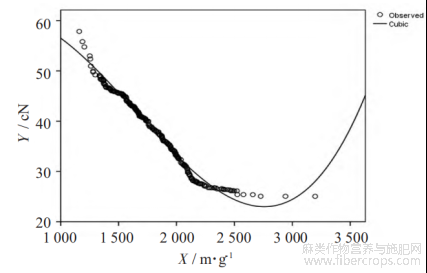
由表1可知,纤维断裂强力与其细度呈负相关,为了便于分析纤维细度与纤维断裂强力的相关性,共设计了以纤维断裂强力为因变量(Y),纤维细度为自变量的5种常用函数,即线性函数(Linear):Y=b0+b1B、二次多项式(Quadratic):Y=b0+b1X+b2X2、对数函数(Logarithmic):Y=b0+b1lnx、三次多项式(Cubic):Y=b0+b1X+b2X2+b3X3、倒数函数(Inverse):Y=b0+b1/X。采用SPSS19.0统计软件分别对苎麻单纤维的264组试验数据(纤维细度与断裂强力)进行函数模型拟合,得到纤维断裂强力(Y)与纤维细度(X)的5种回归模型与对应相关系数(见表2),函数拟合曲线(见图1)。从函数模型拟合可知,3次多项式(Cubic)的相关系数R最高为0.993(函数曲线见图2),二次多项式(Quadratic)次之为0.988(函数曲线见图3)。对三次多项式(Cubic):Y=52.84+0.031X-3.43x10-5X2+6.92x10-9X3一阶求导得:Y'=0.031-6.86x10-5X+20.76x10-9X2,令0.031- 6.86x10-5X+20.76x10-9X2=0,得驻点X1=525,X2=2779,可知单调递减区间X(525,2779)、单调递增区间X(0,525)与X(2779,+纳)。对二次多项式 (Quadratic)Y=107.58-0.054X+8.55x10-6X2一阶求导得:Y'=-0.054+17.1x10-6X,令-0.054+17.1x10-6X=0,得驻点X=3158,可知单调递减区间X(0,3158)、单调递增区间X(3158,+纳)。由于二次多项式 (Quadratic)与三次多项式(Cubic)的相关系数接近,并结合苎麻纤维细度值定义域实际范围一般在800~3000m/g,确定纤维断裂强力与纤维细度的最佳模型为二次多项式(Quadratic)平方模型:Y=107.58-0.054X+8.55x10-6X2,定义域单调递减区间X(0,3158)涵盖了纤维细度值实际范围,该模型可用于相应纤维断裂强力的计算。
苎麻单纤维断裂强力与细度5种回归模型及相关系数见表2,苎麻单纤维断裂强力(Y,cN)与纤维细度(X,m/g)的5种回归曲线图见图1,苎麻单纤维断裂强力(Y,cN)与纤维细度(X,m/g)的三次多项式回归曲线图见图2,苎麻单纤维断裂强力(Y,cN)与纤维细度(X,m/g)的二次多项式回归曲线图见图3。
表2苎麻单纤维断裂强力与细度5种回归模型及相关系数
|
函数 |
回归模型 |
相关系数R |
|
线性函数 |
Y=77.04-0.021X |
0.970 |
|
二次多项式 |
Y=107.58-0.054X+8.55X10-6X2 |
0.988 |
|
对数函数 |
Y=-40.14+338.68lnx |
0.983 |
|
三次多项式 |
Y=52.84+0.031X-3.43X10-5X2+6.92X |
10-9X30.993 |
|
倒数函数 |
Y=-2.19+70864.73/X |
0.980 |
3.2回归模型验证[6]
另取10个苎麻纤维样分别用传统国标法(GB5886—1986)测定纤维断裂强力,同时用纤维细度仪测定相应纤维样品细度,将测定的细度代入回归模型计算出纤维断裂强力(见表2),并对国标法与回归模型法进行显著性检验(F检验和t检验),检验是否有显著性差异。
图1苎麻单纤维断裂强力(Y,cN)与纤维细度(X,m/g)的5种回归曲线图
图2苎麻单纤维断裂强力(Y,cN)与纤维细度(X,m/g)的三次多项式回归曲线图
F检验:
在选用显著水平α=0.05情况下,F(1.01)<F0.05(19,19)(2.20),2种方法精密度是一致的,即2种分析方法差异不显著。
t检验:
即在显著水平α=0.05情况下,t(0.060)<t0.05,38(2.02),2种测定方法的准确度无显著差异,即2种分析方法差异不显著。
国标法与模型法2种方法断裂强力结果比较见表3。
表3国标法与模型法2种方法断裂强力结果比较
|
样品编号 |
Y1(cN) |
Y2(cN) |
残差/% |
X/m |
*g-1 |
|
1 |
35.50 |
36.10 |
-1.66 |
1888 |
|
|
2 |
29.10 |
28.39 |
2.50 |
2315 |
|
|
3 |
45.20 |
44.12 |
2.45 |
1561 |
|
|
4 |
32.00 |
31.30 |
2.24 |
2133 |
|
|
5 |
52.80 |
52.31 |
0.94 |
1285 |
|
|
6 |
45.50 |
46.45 |
-2.05 |
1478 |
|
|
7 |
54.00 |
53.60 |
0.75 |
1245 |
|
|
8 |
40.12 |
41.04 |
-2.24 |
1678 |
|
|
9 |
25.12 |
24.46 |
2.70 |
2657 |
|
|
10 |
24.51 |
24.00 |
2.13 |
2714 |
|
|
11 |
25.16 |
24.80 |
1.45 |
2619 |
|
|
12 |
30.20 |
29.87 |
1.10 |
2218 |
|
|
13 |
42.95 |
43.50 |
-1.26 |
1584 |
|
|
14 |
23.98 |
24.08 |
-0.42 |
2704 |
|
|
15 |
38.00 |
37.62 |
1.01 |
1820 |
|
|
16 |
40.21 |
40.19 |
0.05 |
1712 |
|
|
17 |
50.10 |
49.19 |
1.85 |
1385 |
|
|
18 |
34.10 |
34.71 |
-1.76 |
1954 |
|
|
19 |
43.00 |
42.35 |
1.53 |
1627 |
|
|
20 |
23.10 |
22.83 |
1.18 |
2914 |
|
|
平均 |
36.73 |
36.54 |
- |
- |
|
|
SD |
9.961 |
9.996 |
- |
- |
|
|
注:Y1按国标法测定的结果,Y1由回归模型计算得到的结果。 |
|||||
4结论
通过断裂强力(Y)与其相应纤维细度(X)函数模型拟合,结合相关系数R和函数求导分析,构建纤维强力快速计算最优回归模型Y=107.58-0.054X+8.55×10-6X2,并通过麻类纤维细度仪快速测 定出苎麻纤维细度代入其回归模型,计算出纤维断裂强力,特别适合大批量样品纤维断裂强力的分析。并对国标法与模型法单纤维断裂强力结果对比分析,两者无显著性差异,该回归模型能够实现对国际法的替换。
参考文献:
[1]冷鹃,肖爱平,杨喜爱,等.苎麻单纤维断裂强力等速伸长测定法研究[J].中国麻业科学,2015(3):148-156.
[2]冷鹃,肖爱平,杨喜爱,等.苎麻单纤维断裂强力统计特征研究[J].中国麻业科学,2014(3):151-155.
[3]国家标准局.GB5886—1986苎麻单纤维断裂强度试验方法[S].北京:中国标准出版社,1986.
[4]中华人民共和国农业农村部.NY/T1538—2007苎麻纤维细度快速测定方法[S].北京:中国标准出版社,2007.
[5]武松,潘发明.SPSS统计分析大全[M].北京:清华大学出版社,2014:214-217.
[6]薛薇.统计分析与SPSS的应用(第6版)[M].北京:中国人民大学出版社,2021:172-180.
文章摘自:冷鹃,肖爱平,刘亮亮等.苎麻单纤维断裂强力回归模型的构建与应用[J].农产品加工,2023(13):49-52.