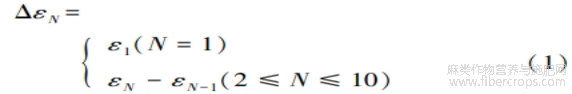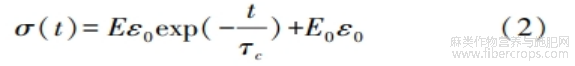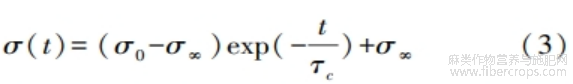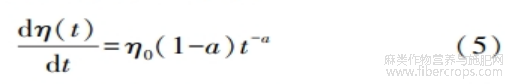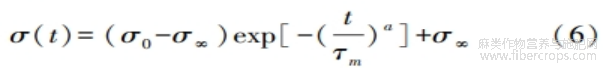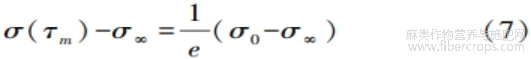摘 要:为深入研究植物纤维增强热塑性复合材料的力学行为特性,基于热压法制备了黄麻织物/聚乙烯复合材料,对其反复应力松弛行为进行研究,分析了初始松弛应力和应力松弛次数对应力松弛行为、应力松弛量、累积应变与应变增量的影响规律。采用定参数和变参数Zener模型对应力松弛实测值进行拟合,比较了预测精度,并分析了变参数Zener模型拟合参数的变化趋势。研究结果表明:应力松弛量、累积应变与各次应变增量受初始松弛应力的影响,同时还与反复应力松弛次数密切相关;相对于定参数Zener模型,变参数Zener模型表现出较高的拟合优度,且可较好地描述黄麻织物/聚乙烯复合材料的黏弹特性参数的变化规律。
关键词:黄麻;织物;聚乙烯;热塑性复合材料;应力松弛;变形;Zener模型
现有研究表明,以黄麻纤维为代表的植物纤维增强热塑性复合材料,具有加工工艺简单、密度小、耐冲击、可回收等优点,在交通运输和建筑等领域具有广阔的应用前景[1-2]。为科学制备和合理使用麻纤维增强热塑性复合材料,研究人员就麻纤维及其与异种纤维混杂增强热塑性复合材料的纤维类型、规格参数、制备工艺、测试条件等因素对其基本力学性能的影响规律进行了较为全面的研究[3-7]。
麻纤维增强热塑性复合材料作为一种典型的黏弹性材料,应力松弛特性是其黏弹性的重要体现之一,也是麻纤维增强热塑复合材料力学特性的重要基础。杨香莲等[8]研究发现,对剑麻纤维进行阻燃和偶联剂处理,可增强纤维与基体材料之间的界面黏结性能,从而提高剑麻纤维增强酚醛树脂热塑性复合材料的抗应力松弛性能。Siengchin等[9]研究发现,相对于斜纹织物和±45°双轴向织物,以单向织物为增强体制备的热塑性复合材料表现出更高的松弛模量;此外,纳米SiO2颗粒填料的加入可进一步提高复合材料的应力松弛模量。韦春等[10]研究发现,剑麻纤维素微晶的加入可显著提高复合材料的应力松弛性能。刘钰馨等[11-12]就增强体纤维含量、应力松弛应变、加载速率对剑麻纤维/聚苯乙烯/丁苯热塑性弹性体复合材料的应力松弛性能及应力松弛后的拉伸强度进行了研究;Mohanty等[13]考虑非线性弹性系数行为、黏性效应和塑性应变,并基于流变元件构建了应力松弛本构方程。此外,汪泽幸等对黄麻织物/聚乙烯复合材料在反复应力松弛下的变形规律[14]、能量耗散规律[15]进行了研究。
目前,对麻纤维增强热塑性复合材料应力松弛性能的研究,多考虑复合材料制备因素对应力松弛性能的影响、应力松弛性能预测模型的构建及循环应力松弛条件下的变形和能量演化规律。但现有研究多集中在单次应力松弛行为,而对反复应力松弛行为及应力松弛行为预测模型的研究较少。基于此,本文以黄麻织物为增强体,聚乙烯为基体,采用热压制备工艺获得黄麻织物/聚乙烯复合材料,并对其在反复应力松弛条件下的应力松弛行为、变形特性及预测模型进行探讨和分析。
1 试样制备与试验方法
1.1 试验材料
以商购黄麻机织平纹织物为增强织物,实测经、纬纱的线密度为242tex,经、纬密度分别68和58根/10cm,单位面积质量为323.60g/m2。
热压制备复合材料前,采用YG747型通风式快速八篮烘箱将黄麻织物在90℃条件下烘干2h,以去除黄麻织物中的水分,避免水分高温汽化,在复合材料内部产生气泡等缺陷。采用SY-6210-B-30PLC程序控制压片机制备黄麻织物/聚乙烯复合材料。双层黄麻织物经纬向交替铺层,并在双层黄麻织物上下两面及之间铺设厚度为0.56mm的聚乙烯膜。在180℃条件下对其预热10min,在180℃、1.0MPa条件下热压5min,然后保压自然冷却至室温,获得双层黄麻织物/聚乙烯复合材料。实测成品厚度为2.43mm,黄麻织物的质量分数为28.92%,换算可知黄麻织物的体积分数为24.21%。
1.2 试样制备与试验方法
因机织物为典型的正交各向异性材料,以其为增强体制备的热塑性复合材料,经、纬向力学性能相似,变形机理一致。为减少工作量,本文仅对经向试样进行测试和分析。沿黄麻织物的经纱方向制备矩形试样,试样宽度为(30±0.5)mm,长度为250mm,有效夹持隔距为(150±0.5)mm。
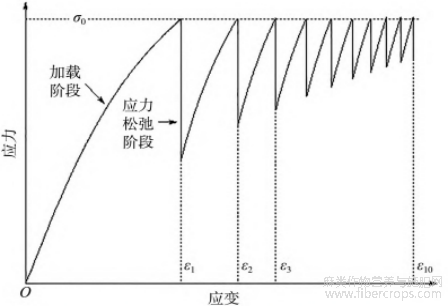
为合理确定初始松弛应力σ0,以5mm/min的加载速率对复合材料的拉伸断裂强度进行测试,5次测试结果的平均值为26.63N/mm2,屈服强度σy约为11.19N/mm2。以此设定初始松弛应力σ0分别约为5.49、10.97与16.46N/mm2,约为拉伸断裂强度的20.61%、41.21%与61.82%。反复应力松弛试验过程中,先以5mm/min的加载速率将试样加载至设定的初始松弛应力σ0,并保持该应力对应的应变,保持时间t∗设定为7200s。此后反复进行加载-应力松弛,设定反复应力松弛次数N为10次,即反复应力松弛10次,每次应力松弛时间为7200s。全试验过程的应力应变曲线见图1。
图1 试验过程的应力应变曲线示意图
所有试验均在温度(22±3)℃的室温条件下,在WDW-20C型微机控制电子万能试验机上进行,选取代表性试样的实测曲线为后续分析对象。
2 试验结果与分析
2.1 应力松弛曲线特性
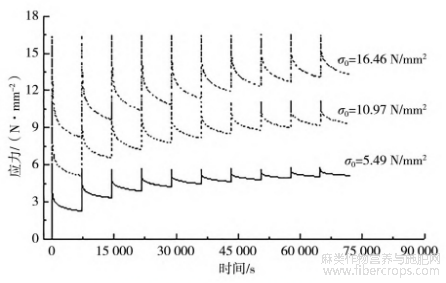
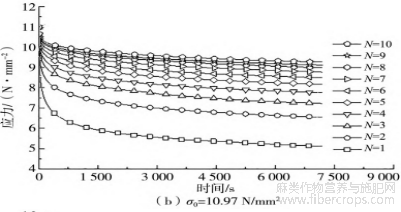
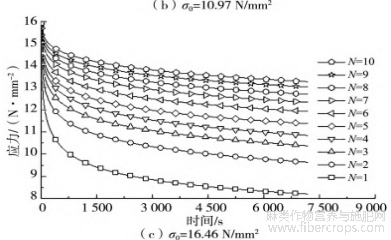
3个不同初始松弛应力σ0下的反复应力松弛曲线绘于图2中。
图2 反复应力松弛全过程曲线
由图2可以发现,同等初始松弛应力下,各次循环的应力松弛曲线形态相似,均呈现先快后慢,之后趋于稳定的变化趋势。该种现象在低初始松弛应力高次循环时表现得尤为明显。此外,即使在较低的应力水平下,试样中的残余应力也未衰减至0,表明黄麻织物/聚乙烯复合材料的应力松弛行为属于典型的非完全衰减型应力松弛。
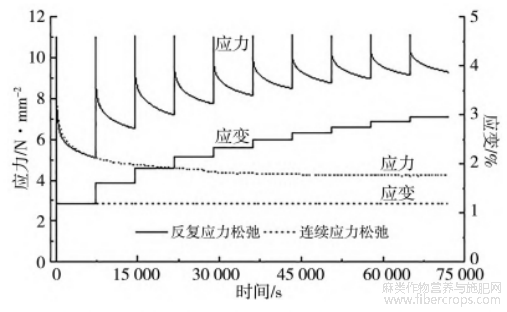
为对比连续与反复应力松弛的异同,以初始松弛应力σ0为10.97N/mm2时的连续和反复应力松弛为代表做进一步分析。其全应力松弛过程的应力-时间曲线以及应变-时间曲线绘于图3中。可见,相对于连续应力松弛过程中试样应变保持恒定,反复应力松弛时,应变随着反复应力松弛次数的增加而呈现阶梯式逐级递增。图3还表明:在初始松弛应力相同的条件下,反复应力松弛过程中首个循环的应力松弛曲线与连续应力松弛曲线高度重合;而在随后各次循环中,试样中的残余应力明显高于连续应力松弛。这表明相对于连续应力松弛,反复应力松弛时,黄麻织物/聚乙烯复合材料表现出较好的抗应力松弛性能。
图3 反复与连续应力松弛对比(σ0=16.46N/mm2)
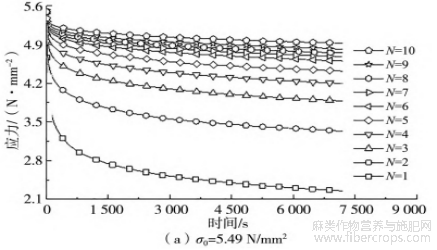
为更清晰地表达不同初始松弛应力σ0下,应力松弛次数对应力松弛行为的影响规律,本文提取了各次循环中的应力松弛曲线,见图4。可见,不同初始松弛应力σ0下,各次循环的应力松弛曲线的形态高度相似,随应力松弛时间t∗延长,曲线均表现出先快后慢的衰减趋势。这表明在反复应力松弛过程中,黄麻织物/聚乙烯复合材料的应力松弛机理一致。
图4 不同初始松弛应力下的各次应力松弛曲线
一个完整的应力松弛循环,包含应力松弛前的加载拉伸阶段及随后的应力松弛阶段(图1)。
试样处于加载拉伸阶段时,随着外加应力的增加,增强体织物和基体聚合物中大分子链发生伸直、伸长;当大分子链的受力超过大分子链间的结合力时,大分子链发生相对位移并产生不可逆的塑性变形;同时,在外加载荷作用下,增强体织物中纱线的纤维发生伸直、伸长、断裂和纤维间滑移,宏观表现为增强体织物结构相的改变。
在随后的应力松弛阶段,外加应变保持恒定,在内应力作用下,随着应力松弛时间的延长,增强体织物和热塑性基体的大分子链可逆弹性变形逐渐回复且可回复量逐渐减少。宏观表现为试样中残余应力呈现快速降低后趋于稳定的变化趋势。
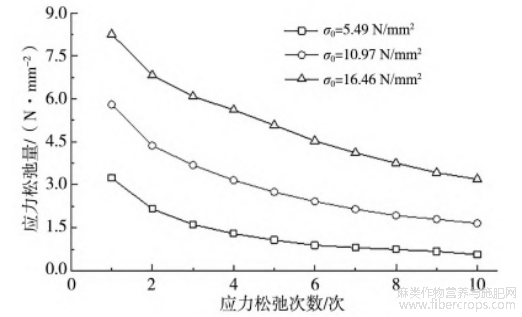
此外,反复应力松弛次数增加,增强体织物和热塑性基体的大分子链可回复的弹性变形量亦逐渐减少。宏观表现为在同等应力松弛时刻(t∗>0),随着反复应力松弛次数增加,试样中的残余应力亦随之增加。故而对于黄麻织物/聚乙烯复合材料,当各次松弛时间t∗为7200s时,各次应力松弛循环的应力松弛量Δσ(Δσ=σ0-σt∗)随初始松弛应力σ0的增加而增加,随应力松弛次数N的增加而减少(图5)。
图5 反复应力松弛时应力松弛量曲线(t∗=7200s)
2.2 累积应变与应变增量
如图3所示,在不同初始松弛应力下,试样应变随应力松弛次数的增加而逐渐增加,该应变为该次应力松弛循环中加载阶段产生的应变与之前循环中加载阶段产生的应变之和,见式(1):
式中:N———反复应力松弛次数;
εN———第N次应力松弛阶段时的累积应变量;
εN-1———第N-1次应力松弛阶段时的累积应变量。
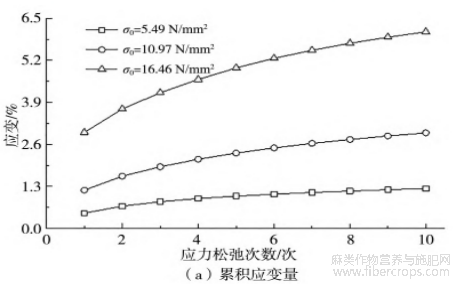
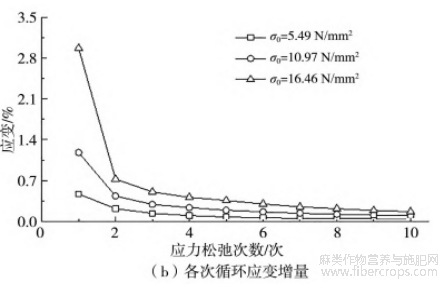
3种初始松弛应力下,试样累积应变N、各级应变增量N与反复应力松弛次数的关系曲线分别绘于图6中。
图6 累积应变量与各次循环应变增量曲线
如图6所示:累积应变εN随初始松弛应力σ0和应力松弛次数N的增加而增加;应变增量ΔεN随初始松弛应力σ0的增加而增加,随应力松弛次数N的增加呈现先快速降低后趋于0的变化趋势。
在同等初始松弛应力的情况下,第1个应力松弛过程(N=1)中,试样应力松弛时保持的应变量为加载阶段产生的应变量;在随后的应力松弛阶段,虽外加应变保持恒定,但增强体和基体内大分子链在内应力的作用下发生构象调整,大分子链中的弹性变形部分回复,大分子链之间产生相互滑动移动,增强体织物中纱线屈曲程度增加,基体部分开裂可能部分闭合。应力松弛持续时间越长,大分子链的回复和大分子链之间的相对滑移亦越充分,增强体织物中纱线屈曲程度回复越充分,基体开裂闭合程度越高。在随后的各次反复应力松弛过程中,因前次应力松弛阶段中增强体和基体的大分子链均已发生部分回复,大分子链之间已产生部分滑移,因此在该次应力松弛过程的加载阶段,试样在外加载荷作用下其增强体和基体的大分子链被再一次拉伸伸长,大分子链之间再次产生相对滑移,增强织物中沿拉伸方向的纱线屈曲程度降低,基体再次开裂破坏。宏观表现为试样应变量继续增加,但应变增加量显著低于前次应力松弛阶段,累积应变量呈现先快后慢的变化趋势。
随初始松弛应力的增加,在各应力松弛过程的加载阶段,复合材料增强体和基体中大分子链被拉伸的程度越大,大分子链伸长程度和大分子链之间的相对滑移量越高,宏观表现为在同等应力松弛次数和相同应力松弛时间的条件下,各应力松弛过程中加载阶段产生的应变量和累积应变量越高。
3 应力松弛模型及其验证
3.1 应力松弛模型与应力松弛方程
图4表明,在不同初始松弛应力及其各次循环应力松弛时,黄麻织物/聚乙烯复合材料的应力松弛曲线的变化规律基本一致且曲线形态高度相似,应力松弛机理一致。故而在反复应力松弛条件下,可用同一模型描述本文黄麻织物/聚乙烯复合材料的应力松弛曲线。
同时,在不同初始松弛应力的各次应力松弛阶段,黄麻织物/聚乙烯复合材料瞬间产生应力降低,表明元件模型中应包含弹簧元件;随应力松弛时间的延长,松弛速率逐渐变缓,最终趋于恒定值,表明元件模型中应包含黏壶元件,即黄麻织物/聚乙烯复合材料的应力松弛具有明显的黏弹性特征。因而可用含有表示弹性变形的弹簧和表达黏性的黏壶构建适用于黄麻织物/聚乙烯复合材料的应力松弛模型。
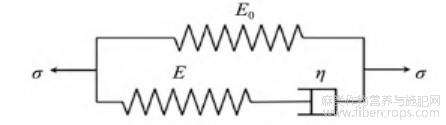
此外,在构建应力松弛模型时,不仅需要考虑模型的物理含义,模型的结构还应尽可能简单、拟合精度高且待定拟合参数少。因此,本文基于1个虎克弹簧和1个Maxwell单元构建了Zener模型,见图7。
图7 Zener 模型示意图
当模型中各元件其黏弹性参数为常数时,即定参数Zener模型的应力松弛方程可表示为:
式中:E、E0———弹簧元件的弹性模量,N/mm2;
η———黏壶的黏滞系数,Ns/mm2;
τc———松弛时间,s,τc=η/E;
ε0———应力松弛阶段材料的应变值,%。
当t=0时,ε(0)=Eε0+E0ε0=σ0;当t→∞时,即材料应力松弛达到平衡状态时,σ(∞)=E0ε0=σ∞。由此,式(2)可改写为式(3):
考虑到初始松弛应力σ0为设定值,因而定参数Zener模型中的待定拟合参数可由式(2)中的3个(E、E0与τc)减少到式(3)中的2个(σ∞与τc)。待定拟合参数的减少,不仅可减少待定参数初值赋值的难度和运算时间,还可提高应力松弛曲线初始段的预测精度。
在外加应力作用下,聚合物及其复合材料的微观结构将发生较为复杂的变化,某些力学性能参数亦随时间的延长而变化。因而,在模型构建时需考虑力学参数的时间效应[16-17]。为简化模型和拟合参数数量的控制,本文仅考虑Maxwell单元中黏壶的黏滞系数随时间的变化函数,见式(4):
式中:η0———非线性黏滞体的初始黏滞系数,η0>0;
a———与外加初始松弛应力和应力松弛时间相关的常数,a≥0。
对式(4)进行求导,可得式(5):
上式中:0≤a0,η(t)为单调递增函数,表明应力松弛过程中黏滞系数逐渐增加;a=1时,dη(t)/dt=0,η(t)=η0,应力松弛过程中黏滞系数保持不变,即为定黏滞系数;a>1时,dη(t)/dt>0,η(t)为单调递减函数,表明应力松弛过程中黏滞系数逐渐降低。
当Zener模型中Maxwell单元中黏壶为变参数黏滞系数时,对应的变参数Zener模型的应力松弛方程可表示为式(6):
当t=τm时,则有式(7):
式中:τm———试样中残余应力衰减至其理论可松弛应力量(σ0-σ∞)的1/e时所需要的时间,即该修正Zener模型的松弛时间,s,τm=(η0a/E)-a。
3.2 模型验证与拟合参数分析
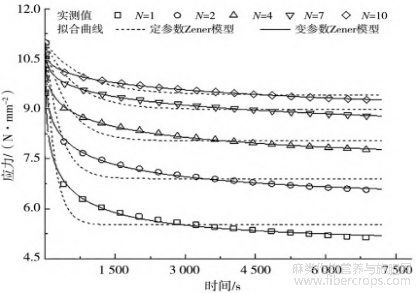
基于定参数和变参数Zener模型的简化表达式,选取初始松弛应力σ0为10.97N/mm2时的实测各次应力松弛数据进行拟合分析,拟合曲线绘于图8中。
图8 定参数及变参数Zener模型拟合曲线(σ0=16.46N/mm2)
从图8可以看出,相对于定参数Zener模型,变参数Zener模型表现出较高的拟合精度,拟合相关系数R2均超过0.99,表明变参数Zener模型可较好地描述黄麻织物增强聚乙烯热塑性复合材料的反复应力松弛行为特性。
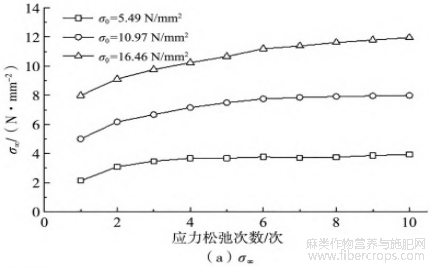
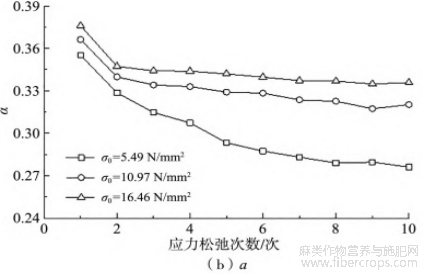
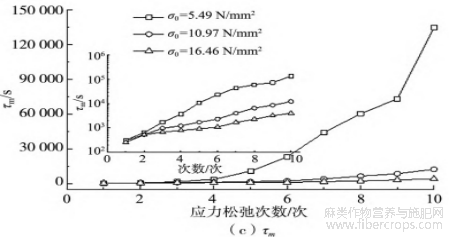
3种不同初始松弛应力下,对变参数Zener模型对各次应力松弛循环的应力松弛曲线进行拟合分析,拟合参数σ∞、a、τm随应力松弛次数N的变化曲线如图9所示。图9(a)表明,应力松弛平衡态残余应力随着初始松弛应力的提高和应力松弛次数的增加而增加。从图9(b)可以发现,对于黄麻织物增强聚乙烯热塑性复合材料,其在3种初始松弛应力、10次反复应力松弛的条件下,拟合参数a均为0~1。这表明在本文试验条件下,黄麻织物增强聚乙烯复合材料在应力松弛过程中的黏滞系数非常数,而呈现逐渐增加的变化趋势。此外,随初始松弛应力和应力松弛次数的增加,松弛时间τm亦呈现逐渐增加的趋势。值得关注的是,当初始松弛应力低于屈服强度时,随着反复应力松弛的进行,松弛时间τm变化较为缓和;而初始松弛应力高于屈服强度时,特别应力松弛次数超过4次时,松弛时间τm快速增加。
图9 修正Zener模型拟合参数曲线
4 结语
本文以热压法制备的双层黄麻织物/聚乙烯复合材料为研究对象,对其反复应力松弛性能进行了测试和分析,主要结论如下:
(1)对于黄麻织物/聚乙烯复合材料,反复应力松弛的各次应力松弛阶段与连续应力松弛的应力松弛机理一致。黄麻织物/聚乙烯复合材料的反复应力松弛行为不仅与初始松弛应力相关,同时还与应力松弛次数密切相关。
(2)反复应力松弛过程中,黄麻织物/聚乙烯复合材料的累积应变随初始松弛应力和反复松弛次数的增加而增加,各次循环的应变增量随初始松弛应力的降低和反复应力松弛次数的增加而减少。
(3)相对于定参数Zener模型,变参数Zener模型可较好地预测黄麻织物/聚乙烯复合材料的应力松弛行为,并可表达反复应力松弛过程中黄麻织物/聚乙烯复合材料的黏弹特性参数的变化规律。
本文仅对黄麻织物/聚乙烯复合材料反复应力松弛各阶段的应力松弛行为,各阶段累积应变与应变增量以及变参数Zener模型对试验时间范围内的预测精度进行分析和讨论。为全面把握以麻纤维为代表的植物增强热塑性复合材料的长期力学行为特性,有必要就复杂受力过程中的应力松弛、蠕变等力学性能变化规律及影响因素做深入研究和分析。此外,还需就黏弹性模型的构建及其对长期黏弹性能的预测精度做进一步研究。
参考文献
[1] ALY N M, SEDDEQ H S, ELNAGAR K, et al. Acoustic and thermal performance of sustainable fiber reinforced thermoplastic composite panels for insulation in buildings[J]. Journal of Building Engineering, 2021, 8(40): 102747. 1-102747. 12.
[2] 秦辉.麻纤维增强热塑性树脂基电子封装材料的研究[D].西安:西安工程大学,2012.
[3] 周颖,罗阳,郭建兵,等.麻纤维增强聚丙烯复合材料研究进展[J].工程塑料应用,2018,46(7):142-145.
[4] 盛旭敏.麻纤维/异种纤维/聚合物复合材料研究进展[J].化工新型材料,2018,46(12):238-241.
[5] 赵鑫,孙占英.超支化聚合物对聚丙烯/剑麻纤维复合材料性能影响[J].工程塑料应用,2021,49(1):120-124.
[6] SHEN J, LI X, YAN X. Mechanical and acoustic properties of jute fi-ber-reinforced polypropylene composites[ J]. ACS Omega, 2021, (46):31154-31160.
[7] GANESAN K, KAILASANATHAN C, RAJINI N, et al. Assessment on hybridjute / coir fibers reinforced polyester composite with hybrid fillers under different environmental conditions[ J]. Construction and Building Materials, 2021, 301(9): 124117. 1-124117. 9.
[8] 杨香莲,韦春,吕建,等.剑麻纤维处理方法对SF/PF共混复合材料动态力学性能的影响[J].高分子材料科学与工程,2010,26(2):95-98.
[9] SIENGCHIN S, DANGTUNGEE R. Polyethylene and polypropylene hybrid composites based on nano silicon dioxide and different flax structures[ J]. Journal of Thermoplastic Composite Materials, 2014, 27(10):1428- 1447.
[10] 韦春,曾思华,黄绍军,等.剑麻纤维素微晶增强酚醛树脂复合材料的制备及性能[J].复合材料学报,2013,30(S1):306-310.
[11] 刘钰馨,梁泽升,吴傲,等.拉伸作用对剑麻纤维增强SBS/PS复合材料的影响[J].现代塑料加工应用,2021,33(2):1-4.
[12] 吴傲.SBS/PS/剑麻纤维复合材料的制备?结构与性能研究[D].南宁:南宁师范大学,2019.
[13] RUBIO-LÓPEZ A, HOANG T, SANTIUSTE C. Constitutive model to predict the viscoplastic behaviour of natural fibres based composites[J]. Composite Structures, 2016,155:8-18.
[14] 汪泽幸,吴波,李帅,等.反复应力松弛下黄麻织物/聚乙烯复合材料的变形特性[J].湖南工程学院学报(自然科学版),2020,30(3):63-67.
[15] 汪泽幸,吴波,李帅,等.循环应力松弛下黄麻织物/聚乙烯复合材料能量耗散演化规律[J].纺织学报,2020,41(10):74-80.
[16] 梁娜,朱四荣,陈建中.一种新的聚合物基复合材料应力松弛经验模型[J].复合材料学报,2017,34(10):2205-2210.
[17] 康永刚,张秀娥,张华明.聚合物应力松弛的非定常微分型本构模型[J].高分子材料科学与工程,2013,29(4):178-182.
文章摘自:汪泽幸,姚航,谭冬宜.黄麻织物/聚乙烯复合材料反复应力松弛行为[J].上海纺织科技,2025,53(02):78-83+110.DOI:10.16549/j.cnki.issn.1001-2044.2025.02.032。