摘 要:为了解长期定位试验下苎麻纤维产量的变化趋势，推动苎麻种植产业增产提效，基于苎麻多倍体1号品种2010—2019年共30个收获期的纤维产量数据，构建ARIMA纤维产量预测模型，并对模型精度进行验证。结果表明:ARIMA(2，0，3)模型最佳，4个收获期中纤维产量预测值与实测值的平均相对误差百分比为7.72%，整体预测效果较好，适用于该地区多倍体1号纤维产量的短期预测

关键词:苎麻;ARIMA模型;时间序列；产量预测

苎麻是多年生草本植物，是我国重要的特色经济作物。课题组利用自回归滑动平均模型(Autoregressive Integrated Moving Average Model，即ARIMA)对长期定位试验下苎麻的纤维产量展开分析和预测，能够探究其长期生产过程中的内在潜力和时空变化，为相关部门制定苎麻产业政策等提供依据。关于作物产量预测研究，常用的方法有多元回归?神经网络和时间序列等，而时间序列方法中采用ARIMA模型的比较多。ARIMA模型主要从变量间的因果关系分析着手，重点探究产量与因素间的相互联系，在产量的短期预测方面有着广泛应用。基于时间序列方法对苎麻纤维产量预测展开的研究较少，且采ARIM模型进行预测分析的更是鲜见报道。

1 试验情况介绍

1.1 试验设计

试验用地位于湖南农业大学国家麻类长期定位试验基地，试验品种为苎麻多倍体1号。课题组于2009年5月采集嫩枝扦插育苗，同年6月移栽，株距45cm，栽培密度3.30×10⁴株·hm^-2，面积20m2，品种重复4次。

1.2 数据选取

选取苎麻多倍体1号2010—2019年所有收获期(每年3个收获期，共30个)的纤维产量数据，另外从2020年?2021年的收获期中各选2个收获期的数据进行比较，验证模型精度。

1.3 处理方法

1.3.1 数据平稳性检验

图1为2010—2019年多倍体1号各收获期纤维产量的时间序列图。由图1可知，虽然多倍体1号的纤维产量序列整体来看围绕某一数值上下波动，但是难以直接判断该数列是否处于平稳状态，因而需要对其进行检验。

图1多倍体1号纤维产量时间序列图

利用Eviews软件对纤维产量时间序列进行ADF检验，结果见表1。由表1可知:ADF统计量的P值为0.01，明显小于0.05，可以认为苎麻纤维产量序列在1%显著性水平下是平稳序列。由此，确认多倍体1号纤维产量序列属于平稳数列，不需要进行差分处理。

表1 多倍体1号纤维产量序列ADF检验表

1.3.2 模型系数的选取

ARIMA模型的表达式为ARIMA(p，d，q)。其中:AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳序列时所做的差分次数。一般通过判断序列的自相关系数(ACF)和偏自相关系数(PACF)的拖尾或结尾情况确定p?q值。由表1可看出多倍体1号纤维产量为平稳序列，因此ARIMA(p，d，q)预测模型中的d值取0，即确定为ARIMA(p，0，q)，最后对模型中的两个参数p和q进行多种组合选择，利用拟合优度R2?AIC和BIC准则评判拟合模型的优劣，从中选择R2最大?AIC和BIC值最小的模型。采用SPSS软件对多倍体1号纤维产量数据进行处理，可知自相关系数和偏自相关系数均存在拖尾现象，可以初步确定模型中p?q阶数为2和3。为找出最佳模型，将p?q阶数为2或3的模型进行比对，相关参数结果见表2。

表2 多倍体1号纤维产量ARIMA系列模型的各项参数构成

由表2可知，所列的9个ARIMA纤维产量模型中以ARIMA(2，0，3)?ARIMA(3，0，3)的R2值最高，均为0.75，其次为ARIMA(3，0，1)，其R2值为0.72，而其他模型的R2值均小于0.70，基本上可以排除。接下来再对上述3个模型的AIC和BIC值大小进行比较:从数值来看，ARIMA(2，0，3)模型的AIC?BIC值分别为89.90?99.70，小于ARIMA(3，0，3)模型的数值93.77?104.98，也小于ARIMA(3，0，1)模型的数值92.98?101.39，因此，可以进一步排除ARIMA(3，0，3)和ARIMA(3，0，1)两个模型，从而得到最优的多倍体1号纤维产量预测模型，即ARIMA(2，0，3)，该模型的相关评价指标如表3所示。

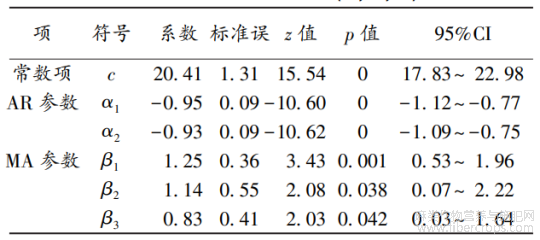
表3 多倍体1号纤维产量ARIMA(2，0，3)模型参数表

1.3.3 模型预测与精度验证

通过对时间序列的分析处理，可以对其未来的发展趋势进行预测[3]。将ARIMA(2，0，3)纤维产量预测模型获取的2010—2019年共30期的纤维产量与实际值进行拟合分析，同时比对2020?2021年4个收获期(每年各选2期)的纤维产量的预测值和实测值，检验模型的预测效果。

2 结果与分析

2.1 多倍体1号纤维产量的拟合结果分析

利用ARIMA(2，0，3)模型拟合的苎麻多倍体1号2010—2019年各收获期纤维产量相关参数指标如表4所示。由表4可知:模型的R2为0.75，RMSE为0.97×10²kg·hm^-2，平均误差百分比(MAPE)为8.41%，小于10%，平均绝对误差值(MAE)为0.59×10²kg·hm^-2，最大误差百分比为32.34%，最小为0.22%，最大绝对误差为2.83×10²kg·hm^-2，最小为0.02×10²kg·hm^-2。多倍体1号纤维产量中的大多数拟合值与实测值接近，表明模型的拟合精度较好。

表4 多倍体1号ARIMA(2，0，3)模型的估计和参数结果

2.2 多倍体1号纤维产量的预测结果分析

将多倍体1号在2020?2021年的4个收获期的预测纤维产量与实测值进行对比，结果如表5所示:4个收获期苎麻纤维产量的绝对误差值分别为0.05?0.03?0.76和1.13×102kg·hm-2，相对误差百分比分别为0.67%?0.45%?9.74%和20.00%，平均相对误差百分比为7.72%，其中2021年三麻的预测精度偏差较大，相对误差百分比为20%；2020年三麻的纤维产量预测精度最佳，相对误差百分比仅为0.45%；4个预测收获期中有两期的纤维产量相对误差百分比小于1%。总体来看ARIMA(2，0，3)纤维产量模型的预测效果较好。

表5 多倍体1号2020?2021年的收获期纤维产量预测精度比对

3 总结与讨论

本文基于苎麻多倍体1号长期定位试验中2010—2021年的纤维产量数据，引入ARIMA模型，同时结合前人的相关研究成果构建了ARIMA(2，0，3)纤维产量预测模型。模型的决定系数R2为0.75，平均相对误差为7.72%，预测精度高于赵嘉宝等和蔡承智等学者研究的精度，对苎麻种植地区无损预测纤维产量有较高应用价值。本研究在构建作物产量ARIMA预测模型时，既不受作物外部生长的环境和气象因素影响，也不考虑生产过程中相关要素的变动情况，主要依托历史产量的时间序列来集中对内外部因素进行动态反应，预测结果取决于序列的平稳性。与传统作物产量预测模型构建方法相比，此预测模型具有数据样本少?运算方便的特点，但在预测效果上存在差异，精度有待进一步提高。苎麻是多年生草本植物，其产量受多种因素影响，因此后续还可以引入多个影响因子，综合运用神经网络?随机森林等机器学习算法开展苎麻纤维产量的组合模型研究，尽可能真实地推演苎麻多年栽种情况下纤维产量的变化。

参考文献

[1] 杨洁，唐昀，申香英，等.我国苎麻产业现状与振兴发展[J].中国麻业科学，2022(4):253?256.

[2] 高卫，张电学，雷利君，等.中国粮食产量影响因素分析及研究方法综述[J].安徽农业科学，2014(33):11954?11955，11958.

[3] 王霞，房少梅.数学建模经验总结[J].教育现代化，2017(21):81?82，87.

[4] 赵嘉宝，陈杰，安霞，等.基于ARIMA模型的吐鲁番市葡萄产量预测分析[J].江苏科技信息，2019(31):34?39.

[5] 蔡承智，杨春晓，莫洪兰，等.基于ARIMA模型的中国水稻单产预测分析[J].杂交水稻，2018(2):62?66.

文章摘自:王辉. 基于ARIMA模型的苎麻纤维产量预测研究[J]. 江苏经贸职业技术学院学报，2023，05.003.